Sets

A set is an unordered collection of objects which are typically referred to as elements or members. What can qualify as an element of a set is fairly broad. Elements can be physical objects such as LEGO bricks. Elements can also be symbolic objects such as the names of Bricklayer functions.

Slides covering this material can be found here.

Bricklayer Sets

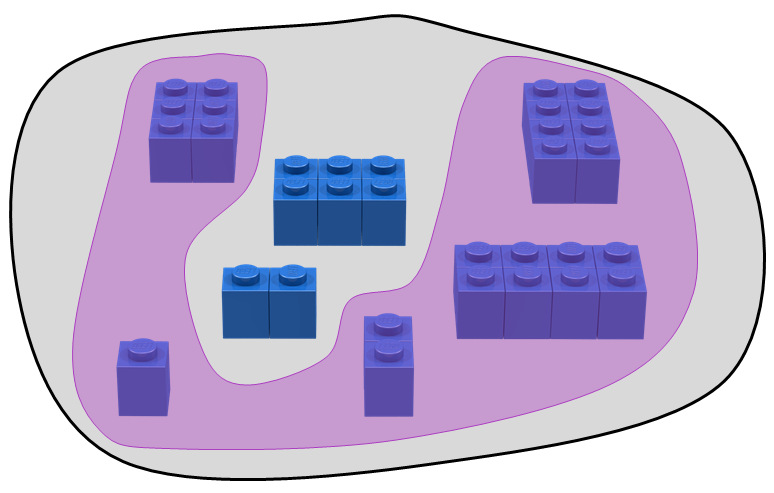
In Bricklayer, there are several kinds sets in which we are particularly interested. Some examples of such sets are shown below.

 

 

 

 

 

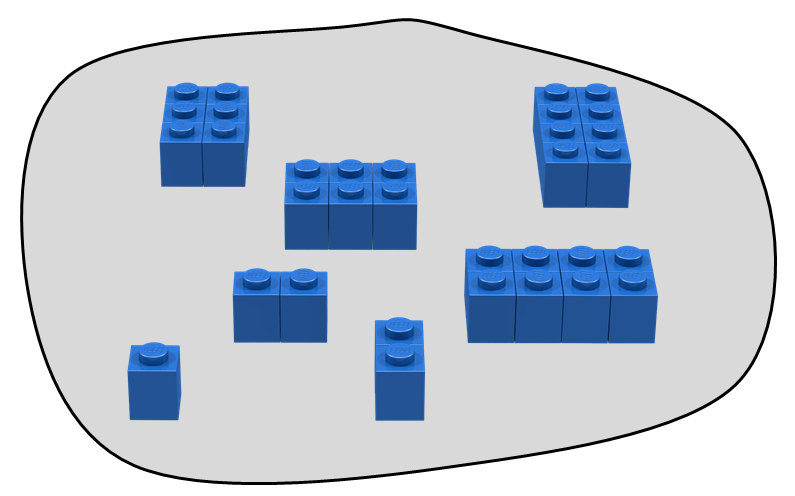
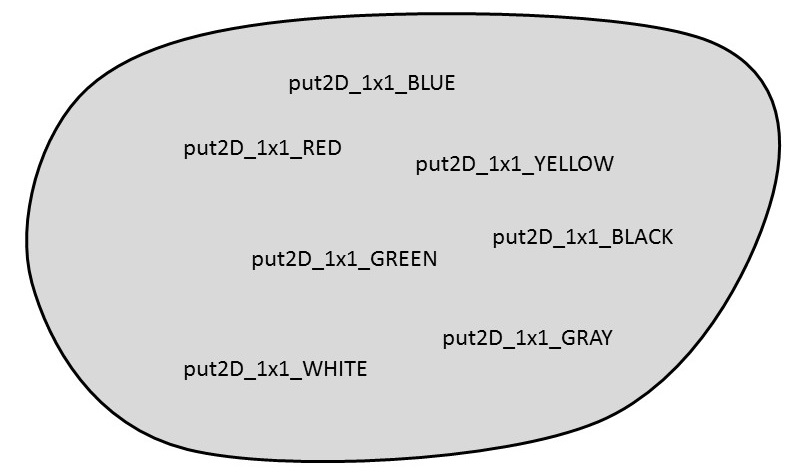
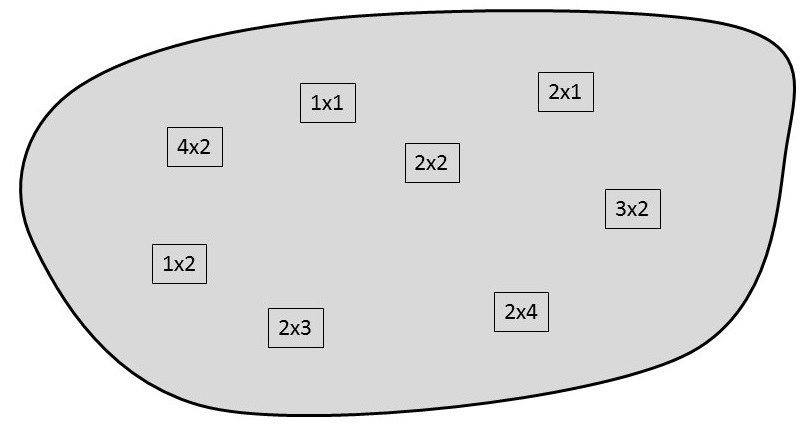
Note that this last set contains elements that can be simplified through computation. In a computational setting, such simplification is often referred to as reduction. For example, the above set contains elements that can be reduced. Also note that elements in the above set which cannot be reduced are integers, and that all other elements in the set can be reduced to integers.

Specifying Sets

When dealing with sets, an important question is “How does one describe/specify a set”? That is, what notation can we use to describe the elements that are contained in a set?

Sets that contain a few elements can be specificed (i.e., described) in, what is known as, a “brute force” fashion by simply creating a list of all elements and enclosing this list in curly braces.

---

Example

The set containing the integers 1, 2, and 3 could be written as follows.

{ 1, 2, 3 }

However, since the order in which elements are listed in a set is irrelevant, the set containing the integers 1, 2, and 3 could also have been written as follows.

{ 2, 1, 3 }

While the above two sets are equivalent, an interesting case to ponder is whether these sets are equivalent to the set shown below.

{ one, two, three }

If we consider the semantics (i.e., the meaning) of the elements , then the answer to this question is “yes”. If we consider the syntax (i.e., symbols) of the elements, then the answer to this question is “no”.

---

 

A brute force approach to the specification of sets does not work well for sets that contain many elements. For example, consider the set that contains one hundred consecutive integers beginning with 1 and ending with 100. It would be quite tedious to create this list integers. In cases like this, the ellipsis symbol can be used to omit parts of an element list that are assumed to be understood. Using the ellipsis symbol, the set that contains one hundred consecutive integers beginning with 1 and ending with 100 can be written as follows.

{1, 2, 3, …, 100}

When using the ellipsis sysmbol in this way one typically lists the first three elements of the set followed by a comma followed by the ellipsis followed by a comma followed by the last element in the set. Infinite sets, can be described by simply omitting the comma and the element following the ellipsis. For example, the set of positive integers can be described as follows.

{1, 2, 3, …}

One can also specify a set using more than one ellipsis sysmbol. For example the set of all integers (both positive and negative and zero) can be specified as follows.

{ …,-1,0,1, …}

Some examples of set descriptions using the ellipsis symbol are shown below.

Brute force description	Description with ellipsis
{0, 2, 4, 6, 8, 10, 12, 14, 16}	{0, 2, 4,…, 16}
{0, 5, 10, 15, 20, 25, 30, 35}	{0, 5, 10,…, 35}
{1, 4, 9, 16, 25, 36, 49, 64}	{1, 4, 9,…, 64}

A problem with the ellipsis symbol is that it is not well-suited for desribing sets whose elements satisfy non-trivial properties. In other words, the ellipsis is only good for describing element lists that follow simple patterns.

One can also specify sets by describing, in some way, the property that an element must have in order to belong to the set. Such descriptions, called truth set descriptions, can be expressed using (1) formal notation – which is more closely looked at in Level 5, or (2) informally using natural language – which we will consider here.

Truth set notation has the following syntax.

{ variable | truth set description }

Typically, the “variable” in this notation is a letter at the end of the alphabet such as x, y or z. Shown below is a truth set description of the set whose elements are even numbers greater than zero.

{ x | x is an even number greater than zero  }

The description above is read as follows: “the set of all x such that x is an even number greater than zero“. In general, when the description uses the variable x, the sentence always starts out “the set of all x“, and the vertical bar translates to the phrase “such that”.

Truth set description	Description with ellipsis
{x | x is an even number greater than zero}	{2, 4, 6,…}
{x | x is a positive number less than 10}	{1, 2, 3,…, 9}

 

Set Membership

The primary operation on a set is membership. Given a set S and an element e we want to know whether  “e is a member of S”.  For the sets that we are (primarily) interested in the answer to this membership question will be either true or false. (It is interesting to note that there exist sets for which the answer to a membership question can be “don’t know”.)

The formal way of asking whether e is a member of S is as follows.

e ∈ S

The expression shown above contains an element e, a set S, and the symbol ∈ which denotes the set membership operator.

Set	Expression	Result
{1, 2, 3}	1 ∈ {1,2,3}	true
{1, 2, 3}	4 ∈ {1,2,3}	false
{1, 2, 3}	two ∈ {1,2,3}	?

Sets are very powerful

Any problem can be restated as a set membership problem.

Example:

• Is 387561 a prime number?
• Does 387561 belong to the set of prime numbers?

It is interesting to note that there exist sets for which the answer to a membership question can be “don’t know”! These kinds of sets can be encountered when writing code.

Cardinality

The cardinality of a set is the number of elements the set contains. Let S denote an arbitrary set. The expression |S| denotes the cardinality of S.

S	|S|
{5,10,15}	3
{a,b,c,d,e}	5
{0,1,2,…}	∞

The set of non-negative integers {0,1,2,…} contains a countably infinite number of elements. The symbol ∞ is used to denote this quantity.

Below are some examples showing the cardinality of some sets that are of interest to Bricklayer.

 

 

Cartesian Product

The Cartesian product of the sets R and S is written R x S and is the set of all possible elements of the form (r,s) where  r ∈ R and s ∈ S. When 2 elements are grouped using parenthesis, their composition is called a tuple. So a Cartesian product will be a set whose elements are tuples.

In vector calculus, a Cartesian product is referred to as a cross product. We will use the terms Cartesian product and cross product interchangeably.

 

The Cartesian Product {0,1,2,3} x {0,1,2,3}.
	0	1	2	3
0	(0,0)	(0,1)	(0,2)	(0,3)
1	(1,0)	(1,1)	(1,2)	(1,3)
2	(2,0)	(2,1)	(2,2)	(2,3)
3	(3,0)	(3,1)	(3,2)	(3,3)

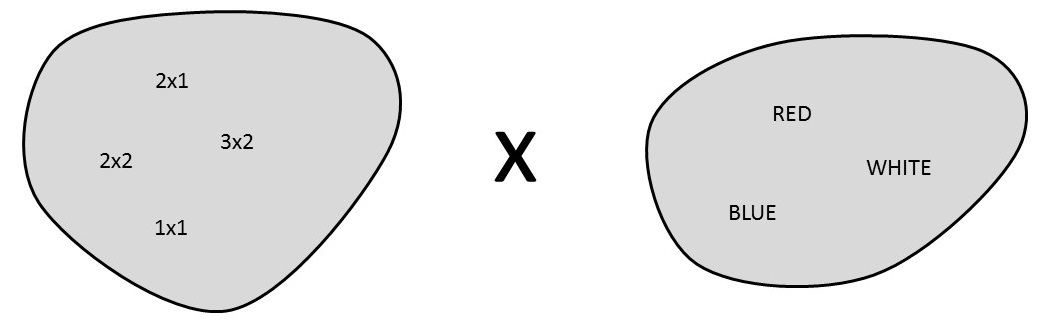
The cross product {1×1,2×1,2×2,3×2} x {RED, WHITE, BLUE}.
	RED	WHITE	BLUE
1×1	(1×1,RED)	(1×1,WHITE)	(1×1,BLUE)
2×1	(2×1,RED)	(2×1,WHITE)	(2×1,BLUE)
2×2	(2×2,RED)	(2×2,WHITE)	(2×2,BLUE)
3×2	(3×2,RED)	(3×2,WHITE)	(3×2,BLUE)

Subset

A set R is a subset of a set S if every element in R is also an element in S. The expression R ⊆ S is an expression whose value is true if R is a subset of S and whose value is false otherwise.

R ⊆ S	Result
{1} ⊆ {1,2,3}	true
{1,3} ⊆ {1,2,3}	true
{4} ⊆ {1,2,3}	false

Note that if |R| > |S| then R cannot be a subset of S.

 

 

 

Note that in the example above the set of integers is precisely the set of all integer arithmetic expressions whose computations are defined. That is, integer arithmetic expressions which can be fully reduced.